1099. Build A Binary Search Tree (30)

时间限制

100 ms

内存限制

65536 kB

代码长度限制

16000 B

判题程序

Standard

作者

CHEN, Yue

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node's key.

• The right subtree of a node contains only nodes with keys greater than or equal to the node's key.

• Both the left and right subtrees must also be binary search trees. 

  Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.

  

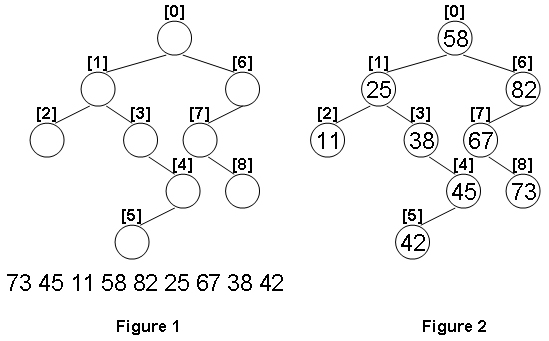
  Input Specification:

  Each input file contains one test case. For each case, the first line gives a positive integer N (<=100) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format "left_index right_index", provided that the nodes are numbered from 0 to N-1, and 0 is always the root. If one child is missing, then -1 will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.

  Output Specification:

  For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.

  Sample Input:

  9
  1 6
  2 3
  -1 -1
  -1 4
  5 -1
  -1 -1
  7 -1
  -1 8
  -1 -1
  73 45 11 58 82 25 67 38 42

  Sample Output:

  58 25 82 11 38 67 45 73 42

• 先建树 再中序遍历 同时数列排序放到对应中序位置 最后层序遍历

#define DeBUG
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <string>
#include <set>
#include <sstream>
#include <map>
#include <list>
#include <bitset>
using namespace std ;
#define zero {0}
#define INF 0x3f3f3f3f
#define EPS 1e-6
#define TRUE true
#define FALSE false
typedef long long LL;
const double PI = acos(-1.0);
//#pragma comment(linker, "/STACK:102400000,102400000")
inline int sgn(double x) {return fabs(x) < EPS ? 0 : (x < 0 ? -1 : 1);}
#define N 100005
int tree[1000][3];
int num[1000];
int k;
void midorder(int x)
{
    if (x == -1)
        return;
    midorder(tree[x][0]);
    //  printf("%d ", x);
    tree[x][2] = num[k++];
    midorder(tree[x][1]);
    return;
}
int ans[1000];
int ansnum;
void layerorder()
{
    queue<int>Q;
    Q.push(0);
    ansnum = 0;
    while (!Q.empty())
    {
        int now = Q.front();
        Q.pop();
        ans[ansnum++] = tree[now][2];
        if (tree[now][0] != -1)
            Q.push(tree[now][0]);
        if (tree[now][1] != -1)
            Q.push(tree[now][1]);
    }
    return;
}
int main()
{
#ifdef DeBUGs
    freopen("/Users/sky/Documents/sublime project/in.txt", "r", stdin);
#endif
    int n;
    while (scanf("%d", &n) + 1)
    {
        int a, b;
        k = 0;
        memset(tree, -1, sizeof(tree));
        for (int i = 0; i < n; i++)
        {
            scanf("%d%d", &a, &b);
            tree[i][0] = a;
            tree[i][1] = b;
        }
        for (int i = 0; i < n; i++)
        {
            scanf("%d", &num[i]);
        }
        sort(num, num + n);
        midorder(0);
        layerorder();
        printf("%d", ans[0]);
        for (int i = 1; i < n; i++)
            printf(" %d", ans[i] );
        printf("\n");
    }
    return 0;
}